深度学习

PhoenixGS
Jul 25, 2022
Last edited: 2023-3-6
type
Post
status
Published
date
Jul 25, 2022
slug
deep-learning
summary
先占坑。哈哈哈，开更咯！（来自半年后
tags
CS
人工智能
机器学习
深度学习
category
icon
password
Property
Mar 6, 2023 02:59 AM
之前看的是《深度学习入门——基于Python的理论与实现》，这次先看了这个视频，发现不是很全，还是再继续看书补充吧

神经网络

神经元

  • a1,a2,…,ana_1,a_2,…,a_n为各个输入的分量
  • w1,w2,…,wnw_1,w_2,…,w_n为各个输入分量对应的权重参数
  • bb为偏置
  • ff为激活函数，常见的激活函数有tanh, sigmoid, relu
  • tt为神经元的输出
使用数学公式表示就是
t=f(WTA+b)t=f(W^TA+b)

感知机

简单的二分类的模型，给定阈值，判断数据属于哪一部分

多层神经网络

  • 输入层
  • 输出层
  • 隐藏层
全连接层：矩阵乘法Y=Wx+bY=Wx+b激活函数

激活函数

非线性函数
  • 线性：
    • f(x1+x2)=f(x1)+f(x2)f(x_1+x_2)=f(x_1)+f(x_2)
    • f(kx)=kf(x)f(kx)=kf(x)
作用
增加模型的非线性分割能力
提高模型鲁棒性
缓解梯度消失问题
加速模型收敛
常见的激活函数
Sigmoid
σ(x)=11+e−x\sigma(x)=\frac{1}{1+e^{-x}}
Leaky ReLU
max(0.1x,x)max(0.1x,x)
tanh
tanh(x)tanh(x)
ELU
x,x≥0x,x \geq 0
α(ex−1),x<0\alpha(e^x-1),x<0
ReLU
max(0,x)max(0,x)
Maxout
max(w1Tx+b1,w2Tx+b2)max(w_1^Tx+b_1,w_2^Tx+b_2)
 
 

神经网络的学习

训练数据（监督数据）&测试数据
避免过拟合

损失函数

神经网络的输出： yky_k ，监督数据 tkt_k
均方误差：
E=12∑k(yk−tk)2E=\frac{1}{2}\sum_k (y_k-t_k)^2
交叉熵误差：
E=−∑ktklogykE=-\sum_k t_k \mathrm{log}y_k

mini-batch学习

从训练数据中选出一批数据(称为mini-batch，小批量)，然后对每个 mini-batch 进行学习

梯度

梯度是各点处的函数值减小最多的方向
梯度下降法(SGD)/梯度上升法
x0=x0−η∂f∂x0x1=x1−η∂f∂x1x_0=x_0-\eta\frac{\partial f}{\partial x_0}\\x_1=x_1-\eta\frac{\partial f}{\partial x_1}
η\eta 表示更新量，称为学习率，是一个超参数

误差反向传播法

数学式&计算图
链式法则

反向传播

简单层
class AddLayer:
		def __init__(self):
				pass
		def forward(self, x, y):
				out = x + y
				return out
		def backward(self, dout):
				dx = dout * 1
				dy = dout * 1
				return dx, dy

class MulLayer:
		def __init__(self):
				self.x = None
				self.y = None
		def forward(self, x, y):
				self.x = x
				self.y = y
				out = x * y
				return out
		def backward(self, dout):
				dx = dout * self.y # 翻转x和y
				dy = dout * self.x
				return dx, dy
激活函数层
ReLU, sigmoid
Affine/Softmax层
Softmax-with-Loss层
 
梯度确认：数值微分与反向传播求出的结果是否一致
 

与学习相关的技巧

SGD

随机梯度下降法
W←W−η∂LW\boldsymbol{W}\leftarrow \boldsymbol{W}-\eta\frac{\partial L}{\boldsymbol{W}}

Momentum

momentum表示动量
v←αv−η∂L∂WW←W+v\boldsymbol{v}\leftarrow \alpha\boldsymbol{v}-\eta\frac{\partial L}{\partial \boldsymbol{W}}\\ \boldsymbol{W}\leftarrow \boldsymbol{W}+\boldsymbol{v}
v\boldsymbol{v} 对应速度，第一个式子表示物体在梯度方向上受力， αv\alpha \boldsymbol{v} 对应地面上的摩擦使物体逐渐减速

AdaGrad

学习率衰减（learning rate decay)
AdaGrad为参数的每个元素适当地调整学习率
h←h+∂L∂W⊙∂L∂W\boldsymbol{h}\leftarrow\boldsymbol{h}+\frac{\partial L}{\partial \boldsymbol{W}}\odot\frac{\partial L}{\partial \boldsymbol{W}}
W←W−η1h∂L∂W\boldsymbol{W}\leftarrow \boldsymbol{W} -\eta \frac{1}{\sqrt{\boldsymbol{h}}}\frac{\partial L}{\partial \boldsymbol{W}}
⊙\odot 表示对应矩阵元素的乘法
故 h\boldsymbol{h} 保存了以前所有梯度值的平方和
变动大的参数的学习率逐渐减小
注：RMSProp，遗忘过去的梯度，指数移动平均

Adam

融合了Momentum和AdaGrad

比较

以 f(x,y)=120x2+y2f(x,y)=\frac{1}{20}x^2+y^2 为例
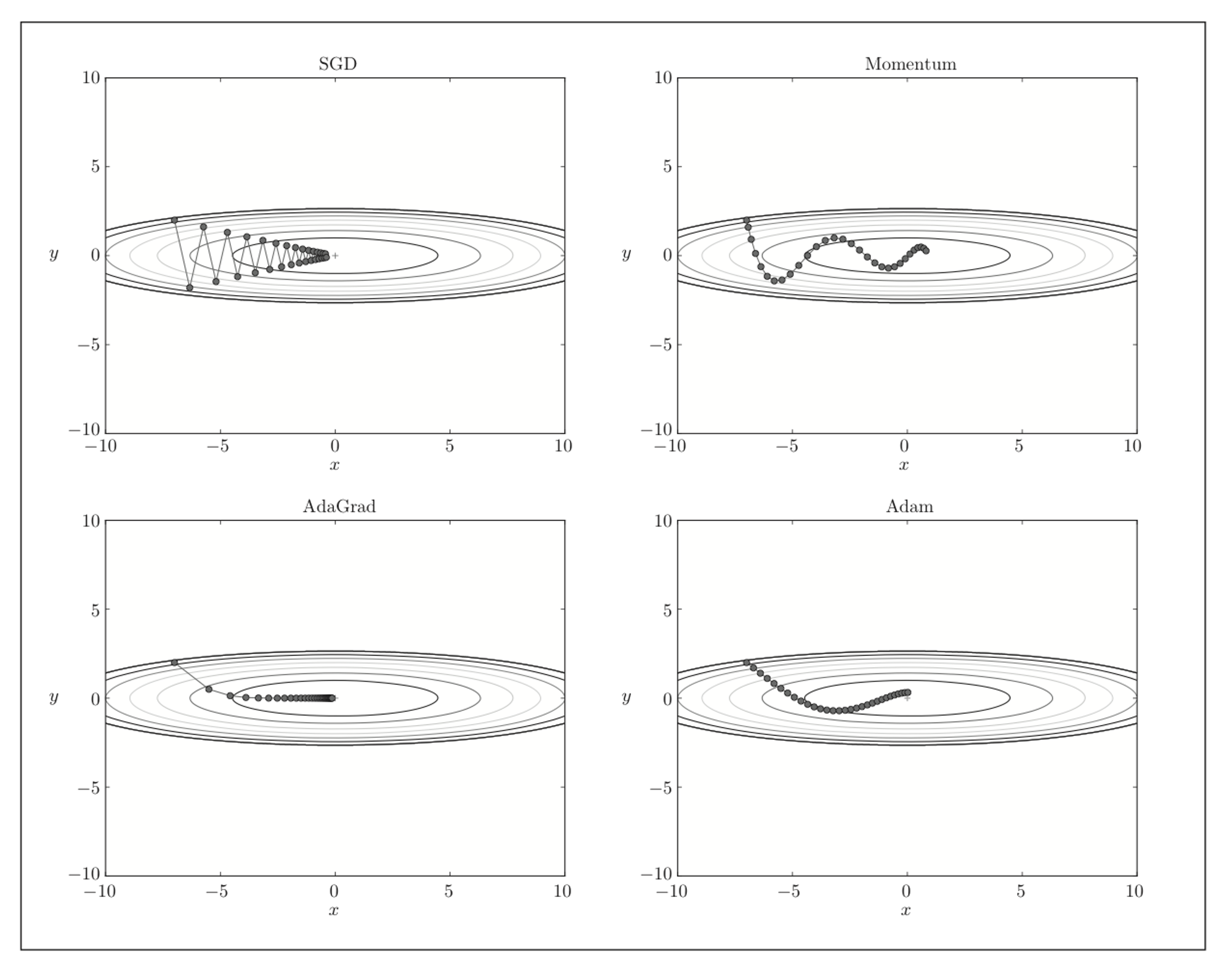
notion image

权重的初始值

正则化

超参数的验证

卷积神经网络

 
 
 
 

梯度

梯度是一个向量，导数+变化最快的方向（学习的前进方向）
收集数据 xx ，构建机器学模型 ff ，得到 f(x,w)=Ypredictf(x,w)=Y_{predict}
判断模型好坏：
loss=(Ypredict−Ytrue)2回归损失loss=(Y_{predict}-Y_{true})^2 \quad 回归损失loss=Ytrue⋅log(Ypredict)分类损失loss=Y_{true}\cdot log(Y_{predict}) \quad 分类损失
目标：调整 ww ，降低 lossloss
自然语言处理tmux使用